Let \(\overline{BD}\) and \(\overline{CE}\) be the altitudes of acute triangle \(ABC\). Let \(\omega_B\) and \(\omega_C\) be the circles with diameter \(\overline{BD}\) and \(\overline{CE}\), respectively. Suppose \(\overline{BD}\) intersect \(\omega_C\) at \(P\), \(\overline{CE}\) intersect \(\omega_B\) at \(R\), \(\omega_B\) and \(\omega_C\) intersects at \(X\) and \(Y\). If \(\overline{XY}\) intersect \(\overline{DE}\) at \(T\), prove that \(\overline{TP}=\overline{TR}\).

Solution

We may look at this problem's original diagram and put \(H\) as the orthocenter of \(ABC\).

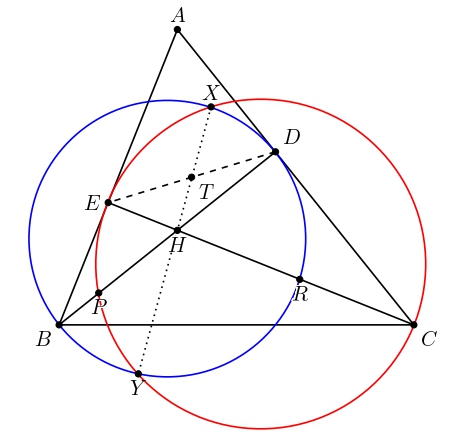
There is a fact that we can show that \(X\), \(Y\), and \(H\) are collinear (I know this from another exercise in some book). We can observe that \(H\) must lie on radical axis of \(\omega_B\) and \(\omega_C\), denote \(\mathcal{R}_{\omega_B,\omega_C}\). We might think it can be shown by Power of Point Theorem or Radical Axis Theorem. To do this, note that \(BEDC\) cyclic since \(\angle BEC=\angle BDC=90^\circ\). Now, we can observe that \(CE = \mathcal{R}_{\omega_C,(BEDC)}\) and \(BD = \mathcal{R}_{\omega_B,(BEDC)}\). By Radical Axis Theorem, we conclude that \(BD\), \(CE\), and \(XY\) concurrent at \(H\). Therefore, \(X\), \(Y\), and \(H\) are collinear.

Why do we deal with segment \(CE\), not line \(CE\)? It's interesting to extend \(CE\) until intersect \(\omega_B\) again at \(S\), and extend \(BD\) until intersect \(\omega_C\) at \(Q\).

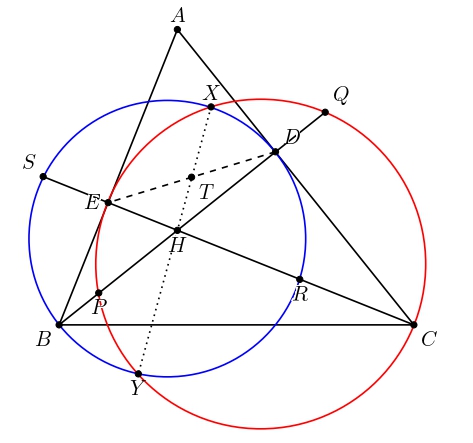
By Power of Point Theorem, we have $$RH\cdot HS = XH\cdot HY= PH\cdot HQ$$ which implies \(RH\cdot HS=PH\cdot HQ\). Therefore, \(P\), \(R\), \(Q\), and \(S\) are concylic. We want to prove that \(\overline{TP}=\overline{TQ}\). If we can show that \(T\) is the centre of \((PRQS)\), we are done. Construct \(B'\) and \(C'\) be the centre of \(\omega_B\) and \(\omega_C\), respectively. If our hypothesis is assumed to be true, we have \(TB'\;\bot\;RS\) since \(RS=\mathcal{R}_{\omega_B,(PRQS)}\) by Radical Axis properties. Analogously, we will have \(TC'\;\bot\;PQ\). From here we will have \(TB'\parallel BE\) and \(TC'\parallel CD\) since \(\angle BEC=\angle BDC=90^\circ\). Since \(B'\) midpoint of \(BD\), we might think consequence of Midpoint Theorem, that is, \(T\) must be midpoint of \(DE\). So, our next goal is to show that \(T\) is the midpoint of \(DE\).

When I wanted to prove directly that \(T\) is the midpoint of \(DE\), it was quite difficult and I thought of using trigonometry (but I was too lazy to do it). So, I thought of assuming \(M\) as the midpoint of \(DE\) and proved it \(M=T\).

Before doing that, we prove that \(M\) is the centre of \((PRQS)\). From the previous explanation, we have \(MB'\;\bot\; CE\) and \(MC' \;\bot\; BD\). By Radical Axis properties, lines \(MB'\) and \(MC'\) through the centre of \((PRQS)\). Therefore, the intersection of \(MB'\) and \(MC'\) must be the centre \((PRQS)\), that is \(M\).

Now, we will prove that \(M=T\). It's equivalence to show that \(X\), \(M\), and \(Y\) are collinear. Note that \(XY=\mathcal{R}_{\omega_B,\omega_C}\). Hence, to show that \(M\) lies on \(\mathcal{R}_{\omega_B,\omega_C}\), we might use the definition of the radical axis. So, we must prove that \(\text{Pow}_{\omega_B}(M) = \text{Pow}_{\omega_C}(M)\) which is equivalence to show that \(B'M^2 - r_B^2 = C'M^2-r_C^2\) where \(r_B\) and \(r_C\) be the radius of \(\omega_B\) and \(\omega_C\), respectively. By Midpoint Theorem we have \(\frac{B'M}{EB}=\frac{1}{2}=\frac{C'M}{CD}\) which implies \(B'M = \frac{EB}{2}\) and \(C'M=\frac{CD}{2}\). On other side, note that \(r_B = \frac{BD}{2}\) and \(r_C = \frac{CE}{2}\). It's enough to prove that $$\frac{EB^2}{4} - \frac{BD^2}{4} = \frac{CD^2}{4} - \frac{CE^2}{4}.$$ By rearranging this equation, it's equivalence to show that $$\frac{EB^2+CE^2}{4} = \frac{CD^2+BD^2}{4}.$$ It's true since by Pythagorean Theorem implies \(BE^2+CE^2=BC^2= CD^2+BD^2\). From here, we have shown that \(X\), \(M\), and \(Y\) are collinear and we conclude that \(M=T\).

Therefore, \(T\) is the centre of \((PRQS)\) and \(TP=TR\) as desired.

Remark

Well, this problem was designed by me for the mock contest Indonesian Mathematical Olympiad on Kontes Terbuka Olimpiade Matematika. I created this problem by messing around with Geogebra. The explanation above is my idea when working on my problem. Many of the contestants like this problem, so that's why I put the title "Cool Problem" xD